If you’ve been coding for a while, you’ve probably come across the term dynamic programming. It’s a popular topic in technical interviews, and it often shows up during design discussions or casual chats with other developers. In this guide, we’ll explore what dynamic programming really means and why it’s such a powerful tool. I’ll use Swift to show code examples, but the core concepts can be applied in almost any programming language
A Different Way to Think About Problems
Dynamic programming isn’t a specific algorithm or coding pattern—it’s a mindset. It’s about how you approach and break down complex problems.
At its core, dynamic programming is all about dividing a big problem into smaller parts, solving those parts efficiently, and reusing their results instead of recalculating them. This approach often leads to faster and more optimized code. It’s commonly used in software engineering challenges where performance matters.
Knowing how to use dynamic programming effectively means recognizing when you can store and reuse previous results—sometimes with a single variable, and sometimes using more complex data structures like arrays, dictionaries, or memoization tables.
Think about how variables work. At a basic level, using a variable to store a value for later is a form of dynamic programming. It keeps you from repeating the same calculation over and over, which saves time and memory. As we’ll explore, this basic concept can scale to solve much more complicated problems.
While the addNumbersMemo function offers a simple introduction to the concept, the true purpose of a dynamic programming solution is to store previously computed values. This approach helps avoid unnecessary calculations, which can be inefficient or even make it impossible to solve certain problems within a reasonable time. This technique of saving and reusing results is called memoization.
Code Challenge – Finding a Pair of Numbers
Over the years, I’ve conducted mock interviews with many developers preparing for roles at top tech companies like Apple, Facebook, and Amazon. Let’s face it—most of us would love to skip the pressure of whiteboard challenges or take-home assignments. Still, these tricky coding questions exist for a reason: they test your grasp of core computer science principles.
Here’s an example of a classic problem that often appears in interviews. It seems simple at first but can reveal a lot about your understanding of data structures and algorithmic thinking.
As developers, we understand that there are often multiple ways to solve a problem. In this case, the challenge is figuring out which numbers in a sequence should be paired to reach a desired result. As humans, we can quickly scan a list and spot a pair like 9 and 2. But for an algorithm, it’s not that simple — it must either compare each number with others or use a smarter method to identify the right values.
The Brute Force Approach
Let’s start with the most straightforward method: brute force. This approach involves taking each number in the array and checking it against every other number to see if together they meet the target condition. For example, if our target sum is 11 and the first number in the array is 8, the algorithm checks if there’s a 3 in the rest of the array (since 11 – 8 = 3). If 3 isn’t found, it moves to the next number, say 10, and looks for 1 (11 – 10 = 1), and so on until a match is found.
Now let’s explore a more efficient solution using memoization. Before jumping into code, consider how keeping track of previously seen values can help us avoid unnecessary comparisons. While we could use a regular array, using a set (also known as a hash table or hash map) is much more effective.
By adopting this memoized approach, we significantly improve our algorithm’s performance. Instead of comparing every number with every other, we store the values we’ve already seen in a set. As we loop through the array, we check if the value needed to meet the target (e.g., target - current number) is already in the set. If it is, we’ve found our pair!
This reduces the average runtime to O(n), since both inserting into and checking a value in a set occur in constant time, O(1). This is one of the key benefits of hash-based data structures—they remain fast regardless of the dataset size.
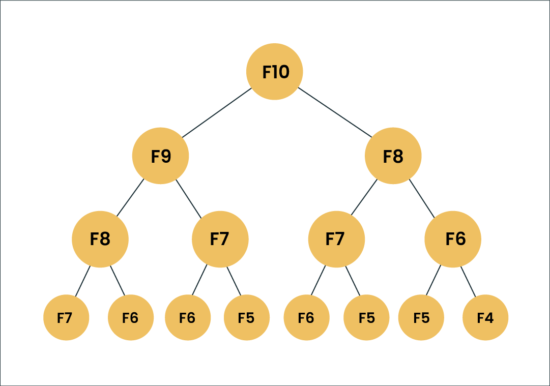
The Fibonacci Sequence and Recursion
When learning advanced programming concepts, recursion is often one of the first techniques introduced. Recursive solutions work by having a function call itself with updated arguments, making them ideal for problems that have a repetitive or nested structure.
While elegant, this recursive solution is not the most efficient—it recalculates the same values multiple times. But just like before, we can improve performance using memoization, storing results we’ve already computed.
As you can see, the number of recursive calls increases rapidly. This exponential growth in function calls happens because the recursive approach recalculates the same values repeatedly—without remembering past results. As a result, performance degrades significantly for larger inputs.
In a production environment, this could lead to serious performance issues or even application crashes. To fix this, we can refactor the code to use memoization—a technique that stores previously computed values to avoid redundant calculations.
A Memoized Iterative Approach
Instead of using recursion, we can implement an iterative version of the Fibonacci sequence that supports memoization. Here’s how the refactored code might look:
Additionally, this iterative solution is easier to maintain and debug. Since it doesn’t rely on nested function calls, it avoids complications with the call stack, memory overhead, and scope management that come with recursion.